Erik Elfgren, Tomas Samuelsson, Anthony Macchiavello
We will look for diverging integrals in QFT and see if they can be made convergent if the space-time is discrete instead of continous. In fact, what is it that really tells us that space-time should be continous? Everything else is quantized, so why not space-time as well?
Finally we will calculate the propagator for a discretized space and compare it with the propagator of the standard model.
In quantum field theory there are several non-explained assumptions and experimental facts that has been imposed on the theory without further understanding. The non-symmetry between right and left particles is one example, the renormalization procedure is another. Renormalization is done in order to get rid of infinite quantities in quantum field theory. The idea is simple, to make theory match experiment an infinite quantity is subtracted from the Lagrangian. At first regard, this seems very strange indeed, but a closer look reveals that it's maybe not that strange after all. Nevertheless, it is quite embarassing to be obliged to add an infinite term without any apparent explanation. In this work we propose a way to get rid of the infinities, even though we don't explain the counter terms themselves. Our proposal is to discretize the space-time so that there is a smallest distance between two particles thus giving a maximum momentum-transfer in an interaction. There are several places in the theory where the discretization would be thinkable. In this report we consider the free propagator in a discretized space with a cartesian discretization with equal spacing in all space-time directions. The discretization is done on the action integral.
For reference and as a gleam of the possibilities of discretized space we also include a summary of an article by Maneolito M de Souza regarding discrete gauge fields and how they can be viewed as a prolongation of our normal guage theory. These fields produce effects just as continuous fields, they are perfectly well determined and they have several other nice properties.
The possibility of space-time being discrete is a fascinating prospect and it opens up a whole new field of thoughts and theories. It could even be the third quantization, just as the particles and later the fields were quantized, so would the space-time be. There are other theories to make the infinite terms finite, but few of them are as revolutionary and yet so simple, as the thought of a discrete space-time.
This first chapter will be dedicated to explaining the basic features of Quantum Field
Theory (QFT). Firstly, we will study the theory of 
theory, though
experimentally not so useful, it provides a simple theoretical framework from which
we can understand the problematics of any kind of quantum field theory, like for example
quantum electro dynamics. The advantage of
the theory is the absence of spin and internal quantum numbers as well
as interactions with other particles which easily clouds the principal features of QFT.
A basic knowledge of the theory of special relativity is assumed as well as a
good comprehension of quantum mechanics.
theory
The theory is the theory of a massive, spinless, self-interacting
scalar particle. The Lagrangian of the theory is given by:
where 
is the wave function of the particle, 
, m is
it’s mass and is the interaction term (the factor 4! is only included
to give the derivatives a nice form, obviously this constant term can be compensated for
with the interaction constant 
). Further on we will use 
, 
and
interchangeably. The power 4 in 
means that for the particle to
interact, it takes three other particles.
Before indulging in the interactions between the particles the non-interacting theory is worth some attention. The Lagrangian of this theory of free particles is
where the index F signifies Free. The action to be minimized is generally given by
(integration over the three space variables and time) where we now have 
. When
the variational equation
is employed to minimize the action, we find the simplest relativistic equivalent to the Schrödinger equation, namely the so called Klein-Gordon equation:
where 
, which is the sum of the second derivatives over
time and space. This equation can be solved directly
by Fourier transformation. The particle is to be interpreted as a free
particle (because there are no interactions), and it is also called the free propagator.
In summary, we have taken the Lagangian, which is the kinetic energy and the potential
energy, applied the variational equations to minimize the total energy and thus found an
equation describing the free particle, .
theory
Let us now attack the self-interacting theory with the Lagrangian given by 
.
With the same procedure as for the free particle we get the variational equation:
which is a non-linear partial differential equation. There is no general way to solve
this equation and to calculate the field we will have to rely on an approximation.
In order to linearize the problem we employ perturbation theory.
What we are interested in here is not primarily to solve the non-linear partial differential equation, but rather to get some results. Hence, we will want to calculate the probabilities of interactions, the cross-sections, through matrix elements like
where T is the time operator and 
is the vacuum field, in the case of n interacting particles.
The amplitude of the action over a path x(t) is given by
which means that the total amplitude at a given time t is
where 
is the integral
over all the possible paths of the particle from point 
to point 
.
In classical mechanics, only the path that minimizes the action would have been
important. Now all paths are important, but the path(s) that minimizes the energy is
the most important one. This can also be regarded in the light of stationary quantum
mechanics. Obviously, all paths must be accounted for, just like all points in space must
be accounted for in stationary quantum mechanics 
.
In our case, not only the path is important but the field (or particle wave function) in
every point in space-time. Hence, we replace the x(t) by 
.
With 
as usual we get
The term 
might look frightening, but as we will see later, it will not
cause any trouble as it will cancel from the normalization.
We will now show that with a specific approximation technique
(called functional integration)
we can get back the free propagator from the free Lagrangian. This indicates that
the method is valid and, in fact, it also holds for interacting fields,
In other words, it can be used to calculate probabilities for outcomes of interactions.
The calculations are done by a Taylor expansion which means that the interacting fields
can be expressed in terms of the free propagator.
The reasoning goes as follows. We add a scalar function 
to
the Lagrangian, thus giving the integral over all possible paths as:
In order to calculate this, we must put the modified Lagrangian
on a quadratic form. First we
concentrate on the term 
. Differentiation of
gives:
from which we can obtain 
as
However, total derivatives, , does not contribute
to the action, which leaves us with the quadratic form:
The kinetic term is now 
and our next step is to incorporate
the differential operator 
in our field thus redefining the field,
so we would get something like 
. The change of variables is
where 
, 
.
K is defined in that way because
This means that we have accomplished the appropriate change of variables in momentum space. For a more rigorous derivation, see Nash [1], p. 32f. As for the other terms in the modified Lagrangian, we absorb them in a similar manner, but we refer again the interested reader to Nash [1], p. 33f.
Finally, we arrive at the equation
where D is the Fredholm determinant, the equivalent of the Jacobian in 
and
is defined as
which is nothing else than the usual scalar particle Green's function.
The only difference between the Klein-Gordon equation and this equation
is that the particle in the Klein-Gordon equation is not time-ordered.
We renormalize F[J] as
in order to have F[0] = 1.
It is now fairly easy to calculate explicitly that
which corresponds to a free particle travelling from point 
in space-time
to point 
.
In analogy with the case of two derivations, 2n derivations corresponds
to n free particles.
We also see that derivation an odd number of times always gives zero.
Finally, for the free fields, n free particles is also written as
, giving us
It can be showed that this means that
can be used as a "basis" for a functional variant of Taylor series expansion.
This property shall be used to expand the interacting version of F[J]
in terms of free propagators.
Let us now turn to the interactions. We use the same type of functional but
replace the free Lagrangian with the total, 
Lagrangian, thus
the interacting version of F[J] becomes
Expansion of the numerator and denominator in terms of means that
we can evaluate, e.g.
which gives the first order terms in the interaction, which can be expanded in terms of
and
which are two and four particles interacting respectively as we get
from equation .
As stated above, this can be proven to give the same result as Feynman perturbation expansion,
and the theory has been validated rather thoroughly.
In this section we have derived a technique for making calculations with a Lagrangian with an interaction term. Without approximation, there is no known way to solve this, but perturbation theory is known to give results in excellent agreement with experiment. The perturbation theory here employed uses functional integration to derive the solutions in terms of the free propagator.
There are several different sources of infinities in quantum field theory. Some are more severe than others but even the less serious ones are rather uncomfortable. The task of making a sensible theory of the infinities is called renormalization. For some of the renormalizations it can be argued that they should be present even in the absence of infinities, for others that our physics of today may not be appropriate. In any case, the answer to what is really going on is still an issue of uttermost interest.
Here is a list of the known infinties in the quantum field theory for the theory.
Even though there is no practical application of the theory, the same
principles and types of infinties are encountered in other field theories, like quantum electro
dynamics. The infinities will be explained in more detail below.
instead of in 
These graphs can be illustrated with e.g. the four-particle interaction term, equation .
which can be calculated to be
In the light of the results from the end of chapter
we can see that this represents four particles, and it is (in principle) represented graphically as in figure
Figure: Interaction of four particles, the graph to the right represents a vacuum
graph.
The first part is only two free propagators just as discussed in the end of chapter 1. The second part is
(cf. eq. ), which is the so called vacuum-graph.
In general, a vacuum graph is a graph with no external legs, a closed graph.
This means that there are no particles entering, nor coming out of the interaction,
it is produced and annihilated in vacuum (but with the other particles as catalysts).
Solution: In the functional method described in the last chapter, the
vacuum diagrams cancel with the 
in equation .
In the usual methods the vacuum graphs have to be dicarded as representing an unmeasurable
phase for the S matrix elements.
Discussion:This type of infinity, or unmeasurable phase is fairly well remedied with the functional method, though there are still a few question marks about what it really means to divide an infinite quantity with another.
This means that the particle annihilates itself, or that a particle and an
anti particle are created at the same point in space-time, they travel to another
point and then they annihilate. An example of such a graph could be figure
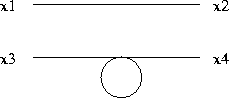
Figure: Self-annihilating particle.
Note the difference between the vacuum graphs described in the previous section and these graphs. Here we have two external legs while we had none before.
Solution:These infinites are removed with something called normal-ordering. This means, basically, that the annihilation operators are placed to the right of the creation operators.
Discussion:This is rather natural as the creation of a praticle always
has to take place before the annihilation. The normal-ordering means that
the does not exist in reality (well, as real as the graphs can ever be.)
instead of in
The Feynman diagrams for the 
theory are quite simple and will be described
briefly. There is only one kind of vertex, and one kind of internal or external line.
The rules for constructing Feynman diagrams are:
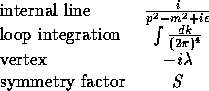
Through a simple graph we will see how renormalization occurs naturaly, even without the effect of canceling infinities. The simplest graph that can be imagined is a line with only two external legs, i.e. the propagator. This graph has the expression
To the second order in the expansion the expression is
where 
is the integral over 
and 
, defined by
To the n:th order in the expansion the expression is
If we use 
and let 
we obtain
Solution:
We notice that the factor 
now plays the role of the mass earlier:
and we define this as being the renormalized mass,
The term 
is usually called the mass-shift and denoted 
.
The mass 
is what we observe in experiments.
Discussion: We have introduced the renormalized mass as a consequence of the interaction, not as a remedy for infinite quantities. Hence, the renormalization is not only a remedy for infinite amplitudes, but exists without them too.
The ultraviolet divergence can be
said to have two sources, that the space-time dimension is four, or that the momentum-
transfer is unlimited, which can be regarded as a consequence of continous space.
There are two principal types of ultraviolet divergence in the
theory, whereof we will only consider
the simpler one. The caculation of the other one is more complicated, and adds nothing
new to our discussion.
The simpler one can be represented graphically as in figure
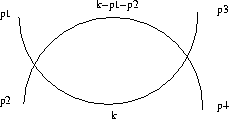
Figure: The ultraviolet divergence appears in this two vertex graph.
With the Feynman parameters and a change of variables, this can be put in the form:
With the use of the formula:
we see that the integral goes towards infinity due to the pole in
in the 
function in m=0.
Solution: In the standard theory, this problem has two
solutions. The classical one is to introduce a cut-off energy, 
and then intergrate to instead of to infinity. Then you add a
counter term to the Lagrangian 
and define the constant A
in terms of so that this will annihilate the -dependent
term from the integral. Finally, you let go to infinity which
does not affect our solution as this is now -independent.
The second method to solve this problem is more elegant at least from
a mathematical point of view. This method is called dimensional
regularization which means that you put 
. You can then
separate the part that contains 
from the other parts. As
before, you add a counter term of the same form in the
Lagrangian but now you let A depend on so that the
final Lagrangian is -independent.
Discussion: It is very unsatisfactory to be forced to add
infinite counter-terms in the Lagrangian to get some sense out of the
equation. The only confort is that the counter term can be interpreted
physically as representing the fact that what we observe is not the bare
particle, but rather the particle with corrections. In the cut-off
method the change of variables required to obtain equation
is not mathematically correct. In the dimensional method we have the
strangeness of a non-integer number of dimensions. What does that really
mean? There is probably no physical meaning in it, but it is still
rather weird. On the other hand, it is not obvious that a discretization
of space would solve the problem either. The discretization takes place
in normal space whereas the infinity appears in momentum space.
Nevertheless, the two of them are so intimately connected that the
discretization of normal space should also lead to a maximum possible
momentum, some sort of natural (in the sense of explainable) cut-off.
The presence of zero-mass particles
in quantum field theory gives rise to a problem
known as the infrared divergence problem. It is not considered to be by far as serious as
the ultraviolet divergence. The reason for this is that it can be fairly well accounted for
in the theory. The infrared divergence is due to the fact that we can always have an infinte
number of photons around every electron, thus seemingly giving rise to an infinite cross-section.
Hence problem here is not in the individual matrix elements, as it was for the ultraviolet
divergence, but rather in the final cross section.
Solution:
However, it turns out that the contribution
from external photons will counter the contribution from internal photons. These photons are
called soft photons due to their low energy ( 
so that no electron-positron pair are
contributing).
For the external photons, the cross section is given by:
where 
is the lower boundary for the photon energy and 
is the cross section without the soft photons and P is a positive constant.
On the other hand, when we calculate the cross section for the internal photons we find it to be:
Hence, the total cross section is given by
where 
represents the part of the cross
section in which only the ultraviolet infinities remain.
Discussion We see that the internal and the external parts of the cross section cancels thus leaving us with a finite cross section (apart from the ultraviolet divergence). The infrared divergence is not a consequence of the space but rather stemming from the photon being massless. Thus, the discretization of space-time would not affect this divergence.
Of the different kinds of infinities we encounter in quantum field theory some of them can be treated fairly well in the standard model (like 2, 3 and 4), while others still give the right results but look very strange and includes bizzare assumptions (like 1 and 5). Discretizing space could be a solution to the strange infinities, but obviously there are also aother candidates. Superstring theory is one possibility, where the point interactions giving rise to the infinities, are replaced by the "nicer" string interactions, or membrane interactions. These need not the renormalization for e.g. the ultraviolet divergence. Either discretization, or superstring theory could also be used to effectively combine quantum mechanics with general theory of relativity, as we're not faced with the problem of renormalization any more. String-theory.
Many problems in physics today are born from the consequence that we look at space-time continuously; we are going to give in a brief overview an introduction to discrete fields by working with the Maxwell theory.
A lot of the calculation and the thinking are going to be left out mainly on the reason that this paper should be short and brief. For further study and questions on the subject I refer to the work of Manoelito M de Souza, Discrete gauge fields.
Let's start by saying that it wouldn't be a problem if everything were to be discrete, because in the bigger scale everything would anyways look continuously. A discrete field gives an illusion of continuity or a macroscopic approximation at a grand scale. Many of today's problems can easily be explain by discrete fields, take as an example wave-particle duality: you have wave-like properties because it's a field and particle-like properties because it's discrete. That's one of the many reasons that discrete fields are interesting and worth take a closer look at.
To start we are going to change only one thing in the standard field theory: instead of a light cone we use a straight line embedded in a 3+1 Minkowski space-time, the light cone generator.
This gives 2 constraints at first look:
Discrete solution to the standard wave equation gives also following properties (these properties are the result from not using light cone support).
From the Maxwell's equations we have (F is an anti-symmetric tensor):
Imposing the gauge condition 
, which is an integrability condition for eq.4
we get:
All thought one can see from eq.1 and eq.2 that gauge freedom and charge conservations are consequences of the anti-symmetry tensor F, with discrete theory one can show that they are not consequence of the anti-symmetry even if you needed to have gauge freedom (last chapter).
To properly define the discrete field in a covariant way causality is used.
This relation describes the free evolution of an interacting field between two
interaction events. Note that hyper-cone is used and not light-cone, the propagation
of the physical objects is constraint so each of its moving points is on a world-line
tangent to a generator of its hyper-cone. With a little algebra and defining
f as a constant four-vector tangent to the hyper-cone, 
, we get:
The tangent of 
is defined as the hyper-cone generator, which one gets from eq.7
& eq.8. With this two equations we see space-time causal structure as a congruence
of lines, a set of points.
A lot of information can be taken from eq.7 and eq.8, for example using the following constraint (using eq.8 for a mass-less field):
We get a constraint between the direction f (the direction of the emitted signal) and the change in the charge state of motion at the time.
Where 
and 
.
This equation hold for all kinds of fields and sources and it's also the cause behind results like the conservation of laws among others.
Because fields are tied to the proper time of their point source we get with
eq.7 and using 
:
Making an explicit dependence 
on A(x) to implement local causality, who itself requires
a field support on hyper-cones. We get 
to be:
And solving the resulting equation with the discrete Green's function we get:
As we can see the point signal here propagates on a straight line f.
The reduction of the field support from a light-cone to a light-cone generator reduces the discrete fields to just a point in the phase space.
Comparing the discrete Green's function (15) with normal Green's function we
can se directly that there exist no singularity in the discrete one 
the field propagates without changing the amplitude. A solution of eq.13 with
the discrete Green's formula gives with 
after some calculations:
Where 
, 
and f & 
are opposing generators in the same light-cone.
This equation has 2 solutions b=1 and b=2 corresponding the creation and annihilation of discrete fields.
Equations 15 and 17 give all fields the constraint that they cannot be independent of their sources. The discrete field is not a gauge field because it's determined only by its source. Since it has no gauge freedom it isn't a gauge field.
Now we are going to use the following equation, for the proof of this formula we refer to the original work.
From the equation 18 we can see the relation between the discrete and the standard field
Giving the conclusion that A is a smearing of over the light-cone and shows
an average of the discrete field, it only can give a "true"
description at large quantities of for example photons in an electromagnetic wave.
On the other hand all the information about f is lost smearing process.
Look at picture; the false picture that A(x) gives is the root of the problem at short distances.
To show that gauge freedom and charge conservations are consequences of the extended causality and Lorentz covariance we calculate eq.13 with a mass-less particle, let's say a photon. The mass-less particle ignores eq.3, i.e. the information about the Maxwell tensor structure, in other words ignoring the connection between the gauge symmetry and charge conservation.
We get the following equation:
We want to show that the Lorentz's condition
is not a consequence of the continuity equation,
and that both are instead consequences of the properties of a discrete world.
With the four vector current given by:
using eq.8 and b=+1 we come after a while to the following expression:
This equation tells us many things. It's both discrete and differentiable, it has both space and time derivatives. This is the reason why the wave-like and particle-like properties in an object are possible.
This is also a universal field, and it is the only solution for a point source.
Further with t=0 and t>0 these equations becomes:
The constraint in eq.10 is a consequence of extended causality and it's a constraint between the direction of propagation and change of motion. Equations 21 and 22 are both consequences of 10. We know that there is a causal link, which doesn't depend on the field tensorial or spinorial nature, between the discrete field and it's source that leads to eq.21 and eq.22.
By using a vector field defined by (for a discrete current for a spin-less electron):
Regardless Maxwell's equation, the F we have charge conservation = Charge conservation is a consequence of extended causality and not gauge symmetry.
To sum it all up, a finite and consistent field theory requires a light-cone generator as the field support, so is defined by causality using a hyper-cone instead of a light-cone.
From eq.10 we can see that is not a gauge field and doesn't have any "singularities".
The traditional continuous field A is an average of the discrete field, we can see that from eq.19. The null f direction is the one to one link that links the field event to the source event, this link is loss in the integration when we are acquiring A from. From eq.19 we can see that the field A that we get is a gauge field with "singularities". The generic fibre f, that actually is a (1+1) manifold embedded on a (3+1) Minskowski space-time, in the integration is replace with the usual light-cone. The result of this is that the point charge event becomes suddenly linked to an infinity of field events.
Why this idea with discrete fields should be investigated more carefully goes without saying. Just only by studying the universe in this way, it can give us an understanding of how the world around us works.
The Klein-Gordon-equation can be written in the form
where 
is a source term.
We can express the wave-operator 
as 
,
where 
and 
and
and 
is the vector 
.
Space can be discretesized in many ways. Here we will only count
the interaction from the closest neighbours and from the closest time.
There are two ways to do that, to the 'right' and to the 'left'.
We can write this mathematically as
where |a| is the space lenght between the points.
By letting 
,
the Klein-Gordon equation will be discretesized as
Explicitly, with equal spacing a, and time-spacing 
the
equation becomes
Probably, the equation has to be solved numerical, especially when the term g is nontrivial. In the continous case, Feynman graphs gives us the method to calculate the solution by perturbation method. So far we are dealing with uncomfortable infinities, for instance the free propagator. Instead of trying to find new mathematics, we will only derive the propagator in our discrete space-time and try to see if it contains any infinity.
Previously, we stated that the action for a free particle in the Klein-Gordon equation is
Discretizising the space will turn the action into a sum. In
our 
and 
operators, we put the scalar
a equal in all directions. This gives us the discrete action as
where now 
.
To derive the propagator we wish to operate in k-space.
One familiar relation between spatial-temporal space (or n-space)
and wavevector space is the four dimensional Fourier transform
In the case 
, we have to sum over all directions to
get the correct transform. We write that transform in k-space as
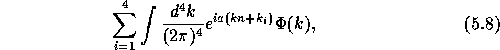
where the vector 
denotes the difference of phase in the i:th
direction. Figure illustrates the case of two
dimensions.
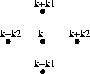
Figure: The k-vectors around a point on a two-dimensional lattice.
After an appropriate transformation and some manipulation,
the operator 
becomes
Expression , can be regarded as a convolution and we then get
The propagator, 
, is defined in chapter 2 by
To find the propagator we transform both sides into k-space.
After a transformation, the right
hand side can be identified as equation and
the left hand side is unity. Thus
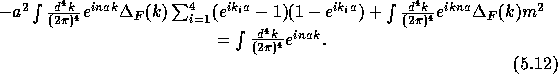
Then we can identify the propagator as 
and
extraction gives us the propagator,
which can be written as
The continuous limit of this discrete propagator is
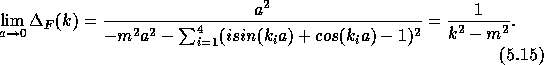
In the continuous limit this is in agreement with the propagator in the standard model.
We put a=1, m=1 and consider only one
wave vector dimension. In figure we plot the discrete propagator
expression with the continous one.
We can truncate the k-number because of periodicity and only take the
intervall 
. As we can conclude from the graph, the
continous propagator has, as expected, two infinities, namely when |k|=1.
Our discrete space does not have any infinities, but the global
maxima lie at the same k-numbers and then turn down.
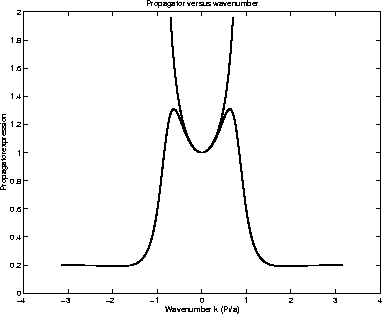
Figure: Continous propagator (upper curve) and real part of
discretesized propagator (lower curve) plotted.
When is the effect of the eventually discretizied world detectable?
So far 
has been tested, and no sight of a non-
continous space. If we put 
into 
we get
which gives an energy of about 0.1 GeV.
If we assume a distance between the points to be the Planck length
, the caracteristic wavenumber for
eventually effects to be notacible is about 1/Planck lenght, roughly
. This gives av energi of about 
, which is at
the scale of the expected GUT-theories.
So far we have considered the effects of a discrete space-time with one space dimension and onetime dimension. However, this is a very simplified model and in a four dimensional theory the structure of the discretization also has to be acounted for. Our first guess would be that the coordinates are aligned in a cartesian manner because this is the easiest model. On the other hand, the points might as well have other configurations, maybe of unknown form. For example, do they have to be aligned to a specific pattern at all? Maybe they are just defined in conjuction with each other, thus leaving the structure undetermined. This can be argued in analogy with quantum mechanics and also quantum field theory, where the particles and the fields respectively are quantisized and thus undetermined. Maybe the discretization of space-time could be the third quantization? This would mean that the uncertainty of the coordinate-points follows some sort of Heisenberg's uncertainty principle, intriguing, indeed. Maybe the coordinate points have an energy, just as particle has an energy even at rest. It is a well known fact that matter bends space-time, could this be an effect due to coordinates with energy? If the coordinates would have energy, wouldn't this also bring the possibility of interactions between them? We could have coordinate waves, maybe bosons? On the other hand this would cause severe complications for our conception of the world. How would the coordinates propagate? However, if the oscillations were significant we would notice a difference in our experiments, thus it should be possible to determine an upper bound for these oscillations. The coordinate energy might even be the missing energy in the universe, the dark matter. The estimated amount of dark matter might also be used to determine limits on the oscillations.
In order to explain the uncomfortable infinities in the standard model, we can also argue that our physics is so far from the high energy scales where we would see a difference, that the physics is entirely different there. Maybe superstrings, maybe a Great Unified Theory or something completely different. But even then, these are not excluding the possibilty of discrete space-time.
The implications and possibilities in a discrete space-time are enormous. Nevertheless, a deeper study in all these things is very complicated and far beyond the scope of this work. We will have to content ourselves with the possibilities, at least for this time.
Consequences of a Discrete Space-Time
(MTF071)
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 -show_section_numbers DiscreteSpace.tex.
The translation was initiated by Erik Elfgren on Mon Jun 26 18:20:28 MET DST 2000
