Erik Elfgren, Tomas Samuelsson
A review on the properties of gravitational waves is presented along with comparisons with electromagnetic theory. Gravitational waves behave very much like light waves, except for that they are second rank tensors instead of being vectors, like light-waves. The different sources of gravitational radiation are discussed, and their origins and strengths. Finally, the development on the experimental front is treated. This is done mainly on the two experiments LISA and ALLEGRO representing the interferometer and the resonance detector types, respectively.
Ever since the introduction of Einstien's general theory of relativity, gravtational waves has been of interest. They arise quite naturally from the theory and were concieved by Einstein himself early after the general relativity. They are, if not an inevitable, but at least a very plausible part of the theory. If they were not to exist, we would have to reconsider Einstein's equations and try to explain why this would be so. This could be an exciting subject for further studies in the area.
Gravitational waves are a natural part of general relativity and astrophysics as they mainly stem from huge gravitational objects rapidly changing form, like supernovae explosions, binary stars revolving about each other, masses falling into black holes and so on.
In 1993, Taylor and Hulse were awarded with the Nobel prize for the discovery of indirect evidence of the existence of gravitational waves. A neutron star looses an amount of rotational energy which currently can only be concieved of as being caused by gravitational radiation. Their measurements of radio waves from a binary pulsar designated PSR1913+16 show that the pulsar's 8-hour orbit around the neutron star is gradually contracting; the faster the pulsar revolves around the neutron star, the smaller its orbit gets. As the rate of decrease agrees to within 0.5 percent with predictions derived from the general theory of relativity, the finding is excellent circumstantial evidence for orbital decay being a result of energy lost by gravitational radiation. Even though the gravitational radiation itself was not detected, Taylor and Hulse shared the 1993 Nobel Prize in Physics for this work.
In this brief review on the subject, firstly some general properties of gravitational waves will be presented. This is done as to acquaint the reader with the concept, and to show the many similarities with electromagnetism, thus facilitating the comprehension of the phenomenon. The second section treats the sources for gravitational radiation without any deeper theoretical argumentation. The principles can be seen easily enough from the end of the first section. Two types of sources for gravitational waves are discussed, periodical and catastrophical. The first being more permanent, the second more intensive. Gravitational waves are currently a hot issue and several attemps of detection is being deviced and put into action. There are mainly two types of gravitational wave's detectors, one technique from the 60's, resonance monitoring, and a second one, more modern, interferometric method. Primarly the next generation of detectors are discussed, where more sophisticated methods for detection are used.
The theory of gravitational waves was originally developed by Albert Einstein 1916 as a part of his extensive study on gravitation. The theory of gravitational radiation resembles a lot the theory of electromagnetic theory. Throughout this section comparisons will be made to show the similarities. When vizualizing what really happens it is often helpfull to think about the gravitational wave as an electromagnetic wave and mass as the charge affected by the field. The reader is supposed to be famaliar with tensor analysis and somewhat with general, or a least special, relativity. If not, Basic Relativity by Mould gives a good introduction to these subjects. We will denote
and
and
Normally, indices 
and 
will be used as dummy indices, while 
and 
will be used for vectors and tensors.
If we neglect the curvature of general relativity
the metric of space-time be written on the form:
where 
is a small perturbation in space-time caused by gravitational waves and
is the normal Minkowski metric tensor:
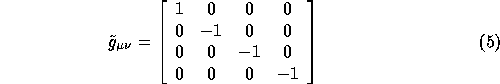
Starting from the Einstein field equations
where 
is the contraction of the Ricci tensor 
, G
is the universal constant of gravitation, and c is the speed of light in vacuum.
The 16 terms of 
is reduced to ten with the symmetry condition 
we have.
In the linearized theory of gravity the Ricci tensor can be written in terms of the metric as
which gives the Einstein's equations:
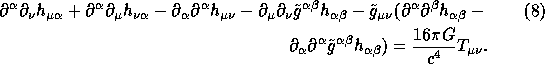
We make a transformation:
and the Einstein's equations takes simpler form:
We can impose the guage condition:
without loss of generality. This can be compared with the guage condition in electromagnetic theory
. The guage condition in gravitational theory eliminates all
but the first term in equation (
) leaving us with the equation:
which can be compared with the equivalent in electromagnetism 
.
With the four guage-conditions, the ten field equations are reduced to only six.
In empty space-time, the energy-momentum tensor of matter is zero, 
. The Einstein's
equations then has the form:
which is a partial differential equation of second order with the solution
where 
is a constant tensor dermining the orientation of the
wave in space. Once again, the analogy with electromagnetism is obvious with
is replaced with 
.
Combining equation () with equation ( 
) the guage condition can now be written as
which means that in the direction of the wave, the field is zero, or in other words, the gravitational waves are transversal. Even with the guage condition there is still a freedom in the equations, since the coordinate transformation
with 
leaves the coordinate system unchanged. This can be used to further reduce
the number of equations, arriving at only two left. These conditions can be arranged in such a manner
that:
which also can be written as
This means that the time-components are all zero and that is trace-less.
With this choice of coordinates, we have defined the Transversal-Traceless (TT) guage.
If we let the wave propagate in the x-direction, 
the TT-guage along with equation ()
and symmetry gives
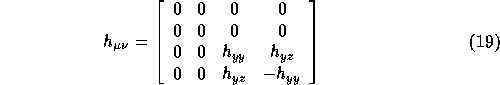
which can be decomposed to
where
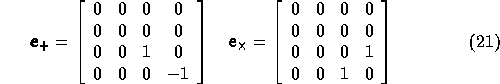
Hence, the wave equation can be split up in rwo components
which are the two polarization states of gravitational radiation.
Let us see what the two states really means. In 
the y-direction
decrease when the z-direction increase and vice versa, see figure . To visualize 
we
rotate the coordinate system 45 degrees where it takes the same form as
is the normal coordinate system. Thus, it represents the same kind of oscillation
but rotated 45 degrees with respect to .
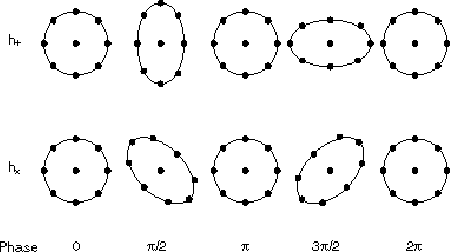
Figure: Deformation of a test ring of matter produced by linearly polarized waves.
With a polarized state 
, the metric of space-time would become
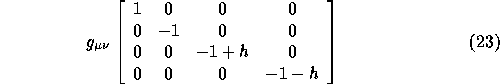
This gives the strain in a material as
This is a summary of what we have seen in the previous section, to better see the similarities.
We have also seen that gravitational waves only have two polarized states which are both transversal, that is, perpendicular to the direction of propagation.
In electromagnetic theory the electric dipole radiation is given by
where L is the luminosity, 
is the electric dipole moment and 
is the charge of particle i.
The equivalent in the theory of gravity is obtained by replacing the charge,
with the mass, 
:
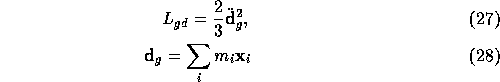
However, 
by conservation of momentum:
That is, there is no gravitational dipole radiation.
The second strongest type of radiation in electromagnetic theory is the magnetic dipole radiation which is given by the second derivative of the magnetic dipole moment:
which would give a gravitational "magnetic" dipole moment of
where 
is the angular momentum. Hence, conservation of angular momentum gives that there is
no dipole radiation for gravitation what so ever.
The first type of radiation that can occur is from the quadrupole moment, and the gravitational luminosity can be expressed as:
where 
is the mass-energy quadrupole tensor of the source:
Gravitational waves, as predicted through general relativity has a number of properties simliar to those of electromagenitc radiation:
There are two types of sources of considerable gravitational waves, periodical and catastrophic. Examples of periodical sources are spinning rods, spinning stars, spinning of asymmetric black holes and double stars. Catastrophic events can be the explosion of a supernova or a strong gravitational collapse. Generally, the energy emitted from the catastrophic events is much greater than that from the periodic sources. However, the very fact that they are periodical makes it relatively easy to monitor them and fine tune our detectors to reduce the noise of the system. Let us start with investigating a couple of periodical sources of gravitational waves.
The energy radiated from a system is principally given by equation ().
To show the order of magnitude of gravitational waves, we will illustrate the power output
from a steel rod of 20 meters length and 1 meter radius spinning as fast as permitted without breaking.
The power ouput for a rotating solid cylinder is given by:
where I is the moment of inertia about the spin-axis and 
is the angular velocity
of the object. For the steel rod, the result is very insignificant:
This tiny energy is then to be distributed among all the particles that it passes which gives a small effect indeed. Of course this was to be expected as we haven't seen any direct evidence of gravitational waves, which we would have observed had the effect been greater. Hence, laboratory-created gravitational waves will not be detected yet for many a year. As we cannot deduce the existence of gravitational waves through a laboratory let us turn to other (natural) sources of gravitational waves.
As previously stated, it is an asymmetry around the axis of revolution that gives rise to
the quadrupole gravitational radiation. Hence, it is only emitted be non-spherical stars
with an asymmetry around the axis of rotation. The asymmetry, e gives a power output
of about
The asymmetry is 
, where a and b are the principal axis in the equatorial plane.
The highest power output will certainly occur for stars with a low radius because this will make the star
rotate even faster, by conservation of angular momentum, thus increasing and consequently
the power output. This fact makes dense objects like neutron stars and black holes a primary
target for detectors. However,
our scope of measurement still lies several orders of magnitude above the calculated power output.
The power output for two objects
of masses 
and 
rotating about each other with an angular
velocity of and a distance between mass-centers of r is
Once again, the angular velocity depends on the radius of rotation, thus conserving
angular momentum. Hence, the closer the two objects are to each other, the higher will the power
output (obviously, they will evetually crash making the formula invalid).
Even if the power output is rather large, it is greatly reduced by the distance between us
and all double-star systems of significance. For example, the binary Per has a radiated energy
of about
which gives
here on earth, which is still a very small value.
About fifty percent of all stars in the universe are belonging to a multiple system. It is estimated
[1] that there should be more than 
double stars in our galaxies with collapsed bodies,
which are more interesting due to their higher angular velocity.
Let us now move on to some catastrophic events, which on one hand gives more energy, but on the other hand are rather short-lived. For an object falling into a collapsed body of mass M, the gravitational energy emitted is
where m is the mass of the object falling into the collapsed body. This energy is peaked around the frequency
For example, a neutron star with mass 
falling into a black hole of mass 
would produce an energy of roughly 
Joules with a peak-frequency of about 6 kHz. If this burst
would occur in the relative proximity of earth ( 
pc) within a millisecond,
it would be possible to observe it with current detectors.
Objects that collapse symmetrically give no gravitational waves. However, the star is rotating while collapsing and bursts of gravitational waves may be emitted during the process. The total energy emitted will depend on the particulars of the collapse, but its spectrum is expected to be continous from zero to the critical frequency
where 
is the density of the final stage collapse and G is the constant of gravitation.
This gives the total emitted energy as
This energy could be considerable and could even be observed if it would occur a major collapse
within our own galaxy. From the Virgo-cluster a few such events are expected per month with an
flux in the order of 
J/s which is within reach of near-future detectors.
There exists two main kinds of gravitational wave detectors: Resonance detectors and interferometer detectors. The first one is able to detect signals at their single resonance modes and the last one can detect signals over a whole bandwith.
In the beginning of the 60's, Joseph Weber build the first
gravitational wave detector. It was a mechanically isolated cylinder
of solid aluminum weighing 1.5 tons. Some piezoelectric strain
transducers at its circumference measured the
vibrations induced by passing gravitational waves.
The bar resonated around the frequence of 1
kHz, which is expected of a gravitational wave from a supernova.
The main problem with resonant-bar antennas is their insensitivity.
The sensitivity was a distorsion of about 
meters.
However, that is too small to detect
gravitational waves from any but the nearest and most violent events.
The noise-level of the detector is measured in strain sensitivity,
and dimension is 
. For an ordinary resonant
detector a noise of 
is a typical number for the resonance modes, but better
technology will hopefully decrease the noise-level to 
in the future.
The detectors are often build of aluminium. To reduce the thermal noise they are cooled down to the absolute temperature and to reduce the seismic noise they are isolated from vibrations.
For an example we have taken the resonance detector, ALLEGRO, in
Louisiana. Schematic description in figure . It is a
cylindric bar cooled down to 4.2K and has a
for f=920Hz and f=896Hz.
The detector is not unique, there are several others of similar character.
In 1978, the first gravitational wave detector to be based on a
laser interferometery
was designed by Forward. It had legs which were two meters long. Five years later,
in 1983, a prototype with 40-meter-long legs was built at CalTech. The
sensitivity was roughly 
. Today the senitivity is even greater,
being is a rather normal value of the sensitivity.
The first generations of large scale-interferometers is under construction; VIRGO in Italy and LIGO in USA. They are expected to start operate in 2002. Two other smaller ones are also being built; GEO300 in Germany and TAMA300 in Japan. Lowfrequency gravitational waves cannot be detected on earth because of the seismic noise. Therefore a space interferometer, LISA, is planned by ESA. One possible target with LISA is to explore the background of gravitational waves from the origin of the universe and probe deeper than we are able to do today. One reason why that is possible is that the graviton interacts very weakly and have a small cross subsection.
The construction of an interferometer detector is simply a Michelson interferometer with very long arms. It is made of optical resonant evacuated cavities with two mirrors, with test masses, at their ends. After going through very long optical path's inside the cavities, two beams of laser light, produced by the same source, are again combined out of phase so that no light gets into the detector. The variation of the optical path length, caused by the changed distance between the mirrors, affected by a gravitational wave, produces a partial phase shift of the beams and, thus, an alteration in the observed luminous intensity which is proportional to the amplitude of the wave.
The lenth of the arms of LIGO are 4 km and for VIRGO 3 km and for the two
smaller ones 300 m. Interferometer detectors are wide-band detectors.
They can measure from a few Hz to several kHz. On the Earth the band
is lowered by the seismic noise. For VIRGO this gives a limit of 2 Hz and for LIGO 40 Hz. Up
to several hundred Hz the thermal noise dominates and after that the laser
shot noise will overshadow this effect. The minimum sensitivity for LIGO is
about 
for 200 Hz and the corresponding for VIRGO is
Hz. All these detectors will be in a network to increase the
reliability and the sensitvity. To be able to detect a cosmic gravitational wave width,
a singel detector with 
is needed.
Obviously, no single detector can detect a gravitational wave. The second or maybe the
third generation of detectors would be able to detect gravitational wave, due to
reduced thermal noise thanks to better technology such as better materials
in the test masses and increase the laserpower.
To reduce the noise, another way is to have a space interferometer, like
LISA, which will have a sensitivity of 
.
LISA will primarly detect gravitional waves from galactic and extragalactic binary systems and generating gravitational waves from massive black holes in the centre of galaxies.
The three flying space craft will act like a giant
Michelson-interferometer, figure , measuring
the distortion of space caused by passing gravitional waves.
Each spacecraft will contain two freely floating test masses. The test masses will define optical paths which are 5 million kilometers long, with a 60 degree angle between them. The precession in optical path will be 20 picometers. The spacecraft are planned to be launched in 2008.
The main problem for LISA is to make sure that the distance
between the test masses is changed only by gravitional waves,
and not by photons and other particles. Therefore the
test masses are carefully isolated from any distortion from
space.
Each of the instument can act like a beamsplitter or a detector,
and the other two will act like the test masses in figure
. Since thay are so far away from each other, they
can't just reflect the beam. Instead the light will be
transmitted to a new beam.
Figure: Gravitaional waves from objects: Coalescence
of black holes (left), black holes orbiting massive black holes
(centre), galactic binaries (right).
LISA will observe gravitational waves from massive black holes; bursts which come from the terminal stages of binary coalescences and continues waves which come from binaries.
Gravitational Waves
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 -show_section_numbers GW.tex.
The translation was initiated by Erik Elfgren on Tue Mar 28 09:28:44 MET DST 2000
