was required and superstring theory was born.
Erik Elfgren, Tomas Samuelsson, Anthony Macchiavello
This report contains a review on the developments in superstring theory. We give a background, introducing the unification and the roots of the present superstring theories. Further, the recent breakthroughs, 1984 with the anomalies cancellation and 1994 with the second superstring revolution, are discussed. Finally we present some possibilities to verify the superstring theories. We also give a short presentation of the few achievable predictions in the theory.
"Strings can sing, So you can think of the world around us as a symphony of strings vibrating in different frequencies"
- Jim Gates
Through the history of the world, many great discoveries and theories have been found by pure accident. In this case the string theory is not an exception.
This complicated theory has from the very beginning required a great deal of contributions from different people, physicits as well a in mathematicians. In fact, a lot of significant work had been done even before the string theory saw the light of day.
In the 19th century Riemann started working with extra dimensions, which is a very important part of the string theory. Around the year 1919, Theodor Kaluza proposed that a fifth dimension could be added to encompass electromagnetism as a mere a consequence of the motion in that dimension. Encouraged by Albert Einstein, Kaluza started to work on his idea that with a fourth space dimension, electromagnetism can be derived from that dimension through it's compactification, i.e. it is thought to be ``curled up'' in a cirle. In 1926, Oscar Klein extended this theory (they both worked independently of each other).
The string theory follows the same idea that the kaluza-klein theory, namely that compact dimensions leads to unified theories (i.e. the unification of forces).
The string theory started in the 1960s in an attempt to describe the strong nuclear force. Its purpose was to explain the relationship between mass and spin for hadrons but quantum chromodynamics was a better solution and became the theory of the strong nuclear force. One of the unwritten laws of physics : if you have many theories and they all work, then choose the one that is easiest. This time QCD was the easiest one. Furthermore, the string theory had many ``difficulties'', like too many dimensions, a really weird particle and so forth. In the string theory the particles arise as excitations of the string. In these, a particle with zero mass and two units of spin appears. This particle has the exact characteristics that a graviton should have in quantum gravity, and so the string theory became related to the theory of quantum gravity.
In 1970 it was discovered that the QM of oscillating strings could
explain the particle spectrum. This marks the actual birth of the
string theory. The string teory was a theory of bosons.
A year later it was realized that to bring fermions into the theory,
a 2-dimensional version of supersymmetry
was required and superstring theory was born.
During that period, several people, like Schwarz, began to see from all the mathematical formulae, that QFT could be described using this new idea. Actually, you can put the graviton particle in QFT but the results you get are just nonsens (with diverging energies and so on).
In the standard model of QFT there are unpleasantly many degrees of freedom and many things that remains unexplained, like gravity. When the gravity is weak enough to allow us to count gravity out, QTF works very well. In fact the standard model only works when gravity doesn't exist at all. This means that gravitation is the major difficulty, and that the standard model is inadequate as a general theory.
The behaviour of interactions in QFT is sometimes impossible to calculate because the forces become singular at short distances. Furthermore, in QTF the interaction of the gravity force happens at a point with no extension. Hence, in QFT the renormalisation sometimes fails. Then we get from the formulae that the force between 2 gravitons is infinite.
The collision between strings happens over a small but finite distance which means that the problem in QFT with the pointlike particles is solved. This also means that we finally are able to combine QM and gravity.
Figure 3.1: Particle physics interactions (left) occur at zero distance, but
string interactions (right) don't.
In 1984 came what is called the first superstring revolution. Among others the work
of Green & Schwarz contributed to the anomaly cancellation[1]. They found that
there were only two ways to construct a consistent theory that were free of
anomalies. These were with the Gauge groups SO(32) and 
.
In the standard model, we know that the amplitude of a process is given by:
where the 
are given by all the Feynman diagrams with n vertices, and g is the
coupling constant (e.g. e in electrodynamics). If we take this to the framework of
strings and demand the theories to be self-consistent (i.e. without diverging integrals
so that 
)
we find that there are only five possible theories. Either the superstring theories
can be based on closed or open strings. The five types, with some of their properties,
are given in the table below.
Table 4.1: The five different superstring theories with their basic features
The fact that there were five, and not one possible theory was an annoyance. Claiming to be the theory of everything, how come that there is more than one theory? Fortunately, this problem has a solution which will be presented in the next chapter.
The action of a point-particle is the integral over a line element (Feynman path integral)
and consequently the action of a string is the integral over a surface.
The strings live in a 2-dimensional space called the world-sheet.
, with 
as the time-coordinate, 
as the
function coordinates, describes the string.
The boundary 1 determine the equations of motion.
For closed string theories, 
.
For (most) open string theory, 
, where
. On a world sheet the action
becomes
, where L is the Lagrangian.
It is possible to obtain the standard model as a limit of the superstring theories
by letting the extra six dimensions curl up in specific ways. This might seem as a
problem but the curled up dimensions can actually be used
to explain things like the
mass, the angular momentum and the electric charge. They simply become a motion in
that dimension, and their value is a function of the coupling constant for superstring
interaction, 
. As a simplification, it is often assumed that the extra
dimensions are wrapped up like circles.
There are a great number of different ways to curl up the extra dimensions, even when we require the theories to have the standard model as their low-energy limit. This is a problem, or maybe an opportunity, for testing the superstring theories.
A major flaw with the string theory was that it wasn't as well described as the Quantum Field Theory. It lacks the 'second quantification'. The second quantification is the quantification of fields, the first is the quantification of particles. Another flaw was that there were five different theories that satisfied the requirements, instead of one.
The five different theories are in fact related to each other through something called
duality transformations, which can be regarded as a generalization of 0
duality.
This result was discovered in 1995 by Hull & Townsend [2]and invoked a new
interest in the theory of superstrings. A duality transformation can bring us from strong
coupling in one of the five theories, to weak coupling in another. We know well how
to study weak couplings with perturbative methods, but strong couplings are difficult.
Hence, with the help of duality transformations, we can study the strong coupling of
one theory with the results from the weak coupling of the dual theory.
Some of the duality transformations leads to an 11-dimensional theory, not previously included in the five because it isn't a string theory. This new theory leads to the idea that the five 10-dimensional theories and the 11-dimensional theory were only different limits of a more fundamental theory, referred to as the M-theory (M for mother). In addition to strings, objects called p-branes are included in the M-theory. The p is the number of spatial dimensions, p=0 for particles, p=1 for strings, p=2 for membranes, etc.
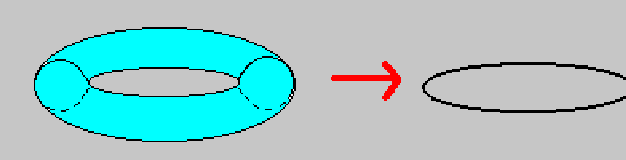
Figure 5.1: The compactification of the 11-dimensional M-theory to ``ordinary'' 10-dimensional
superstring theory.
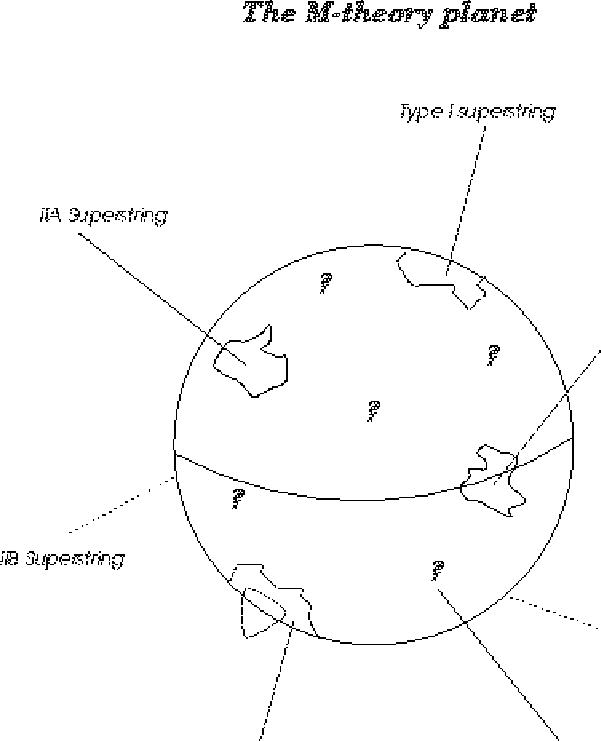
Figure 5.2: The M-theory can be regarded as a planet whereof we have only discovered a couple
of islands
Just as a 1-dimensional string sweeps out a 2-dimensional world-sheet a p-brane
sweeps out a d-dimensional worldvolume, where d = p + 1. Of course,
there must be enough room for the p-brane to move about in spacetime, so d must be less
than or equal to the number of spacetime dimensions D.
Now, the p-branes are described by 
, where 
are the worldvolume coordinates
and M runs from 0 to D-1.
If the superstring theory is to be considered to be a grand final
theory for everything, then we must be able to calculate every physical
constant (masses, charges, angular momenta etc). Today no one knows
how to write down the equations to solve this. Further, among all the string
theories today, we cannot find exact solutions in any one of them.
So far no one has been able to develop the mathematical
tools to solve this problem. If we could derive everything then
this is a good indication that superstrings really exist.
To test the existence of superstrings experimentally we must
have energies in the order of magnitude 
GeV.
Compare this to LHC's 
GeV or the most energetic cosmic particle
ever detected, 
Gev. The radius of curvature is of the
Planck length, 
. Thus, from Heisenberg's uncertainty
principle the energy must be GeV, which is the
energy available for a particle one second after the Big Bang.
In the closest future it is impossible for us to
achieve an energy of GeV - it would require an accelerator
diameter of a few light years.
Fortunately, all hope is not lost as the superstring theories demand GUT (Grand Unified Theory) and SUSY (supersymmetry). This means that if we could prove them, super strings would become an even better candidate to be the unification theory. However, GUT predicts proton decay and since several years, measurements of proton decay are going on. No proton decay has yet been detected, which implies that the simpliest GUT symmetry groups are out. If SUSY exists, then the lowest energy SUSY should be detected in the new particle accelerator LHC at CERN which will start operating about 2005. If the experiments don't show anything, or if they show something totally unexpected then we can say that superstring theory is in serious trouble.
If we have more than four dimensions then we would have Kaluza-Klein echoes which means that particles would have cousines with higher energy. The wavefunction will be bouncing in higher dimensions and we will see them as different particles. This is an unmistakeable signal of more dimensions. If the new dimension have a length of 10 meters then the energyspacing is about 1000 Gev and this should be possible to observed in LHC.
Superstrings include gravity and the most interesting scen for superstring tests in a few year will be in cosmos. Strings can't presently make any useful, realistic prediction in particle physics but in astrophysics many predictions can be made. Examples are Hawking radiation from black holes, time around big bang, theory of inflation and other measurable fenomena. If measurements agree with calcuations then we can at least say that there is something in superstring theory that is true.
An additional Z-boson, Z', is predicted in GUT and is copious in stringtheory. It accurs in compactification of the heterotic string. Recent discoveries at CERN [3] indicate that the properties of Z' predicted from stringtheory gives a better fitting to data in decay of Z.
In this report we present an overview of superstring theory. Obviously, we cannot cover the entire field, but we resume some of the most important features of the history, the present research and the future. Since 1995 the interest in superstring theories has exploded. It seems as a plausible candidate to explain the arbitrariness of the standard model. Some of this work is reviewed my Maharana [9]. The superstrings are exciting phenomena and the theory is beautifully consistent.
The mathematics are very complicated and the research on superstrings has had several spin-off effects in mathematics. In the current M-theory, the five theories are interrelated, and even though the properties of the M-theory so far lies much unexplored, it seems very promising. However, even if the M-theory is extensively explored, we still don't know why the universe curled up the way it did from 11 dimensions to our present 4. Hopefully, though, it might be able to give is hints to this process.
Probably, we never will be able to produce a string, nor write down the fundamental equation(s) for them. Despite that, if the parts we can reveal are consistent and can be used to uniquely explain the standard model and general relativity, we can use the superstrings as a hypothesis until nature disproves us. Maybe the near future (LHC) holds something totally unexpected. Something that rules out as well SUSY as GUT and strings. That would really be exciting!
A Review of Super Strings
(MTF071)
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 -show_section_numbers superstrings2.tex.
The translation was initiated by Erik Elfgren on Tue Mar 28 09:50:09 MET DST 2000